Mistake 6: Using the test set for fine tunning
Most machine learning models require some hyper-parameter tuning. For example, KNN requires to specify the number of nearest neighbors \(k\) and the distance function (Euclidean, Manhattan, etc.). In decision trees, you need to specify the feature importance function, maximum tree depth, etc. For ensembles, you need to specify the number of models, and so on. Parameter tuning can also occur when preprocessing the data. For example, when applying a moving average filter to timeseries data, one needs to define the window size.
Finding the best hyper-parameters requires trying different values either by hand, or by using optimization procedures such as grid search, genetic algorithms, Bayesian optimization, to name a few.
One of the most common mistakes occurs when using the test set to optimize hyper-parameters. Figure 6.1 exemplifies this scenario. Here, the best \(k\) for KNN is looked for. The model was fitted using a train set. Then, different values of \(k\) (1-3) are evaluated using the test set. In this case, the model is being overfitted to the test set.
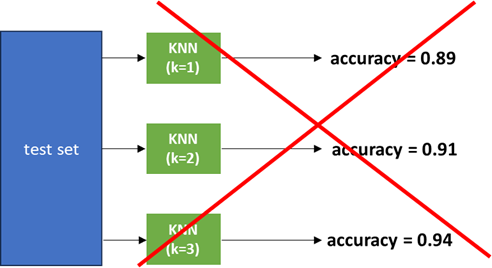
Figure 6.1: Overfitting a model to the test set.
The following code snippet illustrates this same scenario when building a KNN classifier for the WISDM dataset.
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y,
test_size = 0.5,
random_state = 123)
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
for i in range(5):
knn = KNeighborsClassifier(n_neighbors = i+1)
knn.fit(X_train_scaled, y_train)
y_pred = knn.predict(X_test_scaled)
accuracy = accuracy_score(y_test, y_pred)
print(f"k={i+1}" f" accuracy {accuracy:.2f}")#>> k=1 accuracy 0.83
#>> k=2 accuracy 0.79
#>> k=3 accuracy 0.81
#>> k=4 accuracy 0.80
#>> k=5 accuracy 0.80The problem with this approach is that the value of \(k\) is being chosen specifically for this test set. Thus, the model’s performance is likely being overestimated when reporting the accuracy with the best selected \(k\).
The correct way of evaluating different hyper-parameters is to do so using an independent set of data. Typically, this one is called the validation set. Instead of dividing the data into two subsets, it should be split into three subsets: train, validation, and test sets.
The model is trained with the train set. Then, hyper-parameter optimization is performed using the validation set. Once the best hyper-parameters have been found (\(k\) in this example), the final model is tested only once using the test set (and these are the performace measures to be reported). Figure 6.2 shows this procedure.

Figure 6.2: Finding the best hyper-parameters using an independent validation set.
In code, this would look like this:
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = 0.5,
random_state = 123)
# Split the test set into two equal-size sets.
X_test, X_val, y_test, y_val = train_test_split(X_test, y_test,
test_size = 0.5,
random_state = 123)
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_val_scaled = scaler.transform(X_val)
X_test_scaled = scaler.transform(X_test)
for i in range(5):
knn = KNeighborsClassifier(n_neighbors = i+1)
knn.fit(X_train_scaled, y_train)
y_pred = knn.predict(X_val_scaled)
accuracy = accuracy_score(y_val, y_pred)
print(f"k={i+1}" f" accuracy {accuracy:.2f}")#>> k=1 accuracy 0.83
#>> k=2 accuracy 0.80
#>> k=3 accuracy 0.81
#>> k=4 accuracy 0.80
#>> k=5 accuracy 0.80Here, half of the test set used as the validation set which is used to find the best \(k\) (\(1\) in this case).
Finally a KNN with \(k=1\) is evaluated on the test set, and this is what is reported.
best_k = 1
knn = KNeighborsClassifier(n_neighbors = best_k)
knn.fit(X_train_scaled, y_train)
y_pred = knn.predict(X_test_scaled)
accuracy = accuracy_score(y_test, y_pred)
print(f" test set accuracy {accuracy:.2f}")