Mistake 14: Encoding categories as integers
Many machine learning algorithm implementations require all data to be in numeric format. This is the case of neural networks and several scikit-learn models. However, a dataset can have categorical variables as well. For example, clothing sizes: small, medium, large. These can be converted into integers \(1\), \(2\), and \(3\), respectively. In this case, this variable is ordinal. This means that the values have an order: small \(<\) medium \(<\) large. So, it makes sense to encode the values with integers \(1...n\) since those integers represent the fact that small (\(1\)) comes before medium (\(2\)) and so on.
Now, take for example a predictor variable job title with values: dentist, geologist, and accountant. This variable is not ordinal since there is no implicit order between its values. We may be tempted to convert this variable as integers as well. However, doing so can inadvertently assign an implicit order to the variables. Then, how do you convert a non-ordinal predictor variable into a numeric format? Answer: You can one-hot-encode the variable. One-hot-encoding consists of replacing the original variable with \(n\) boolean variables called dummy variables, where \(n\) is the number of unique values. Each new dummy variable corresponds to one of the possible values.
Figure 14.1 shows an example database where the Job title column is categorical. After one-hot-encoding it, you can see that there is a column for each possible job title. Since Ingrid is a dentist, the corresponding column is marked with a \(1\) and the remaining ones are set to \(0\) to indicate that she is not a geologist, nor an accountant.
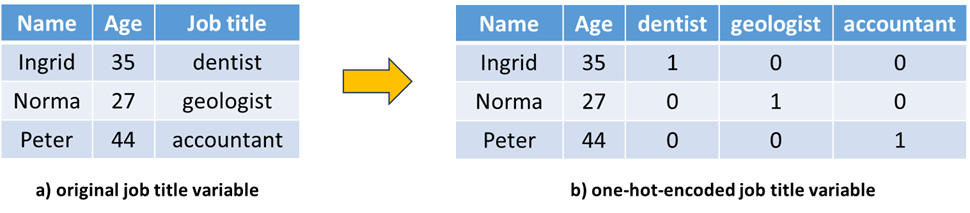
Figure 14.1: Example of one-hot-encoding the job title variable.
When one-hot-encoding a variable that is a predictor/feature, there is something that you need to pay attention to which is called the dummy variable trap. This means that the value of one of the dummy variables can always be predicted by looking at the value of the other ones. For example in the case of Norma, if we know that the columns dentist and accountant are \(0\), we can infer that geologist must be \(1\). Or if we know that dentist is \(0\) and geologist is \(1\), then we can infer that accountant is \(0\) because there can be at most one column with a \(1\). This creates unnecessary redundancies and correlations that can affect a predictive model. However, fixing this is easy; just remove one of the dummy variables (can be any, for example the first one).
The following example loads and prints the INCOME dataset. For simplicity, only four columns are selected. Figure 14.2 shows the first rows.
import pandas as pd
df = pd.read_csv('data/income/adult.data', header = None)
# Only select some columns.
df = df.iloc[:, [0, 1, 7, -1]]
df.columns = ['age', 'workclass', 'relationship', 'income']
df.head()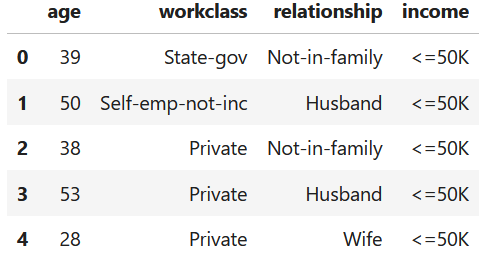
Figure 14.2: First rows of the INCOME dataset.
The relationship column has six unique values.
The relationship column is a non-ordinal variable. So let’s one-hot-enconde it using the get_dummies() function from pandas. The drop_first = True tells pandas to remove the first dummy variable so we avoid the dummy variable trap. Figure 14.3 shows the resulting one-hot-encoded variable.

Figure 14.3: INCOME dataset after one-hot-encoding the relationship varable.
Note that the dummy variables are of type boolean. In some cases, depending on the expected format, you may need to replace True with a \(1\) and False with a \(0\). The following code accomplishes that and Figure 14.4 shows the result.
for col in df_encoded.columns:
if col.startswith('relationship_'):
df_encoded[col] = df_encoded[col].astype(int)
df_encoded.head()
Figure 14.4: INCOME dataset after one-hot-encoding the relationship variable and converting booleans into integers (\(0\),\(1\)).
If you intend to use the workclass column as a feature, then, it should also be one-hot-encoded.
drop_first = False. One-hot-encoding the class is required by some neural network frameworks.